Logistic Regression

Why not Linear Regression ?

---

Imagine that a response is qualitative. Then Linear Regression (Simple Linear Regression) does not perform as well as it does for quantitative for at least two reasons:

1. If a response has more than 2 possible values, then we have problem of ordering them or assigning a dummy variable for each. For example, if medical diagnosis can have 3 responses (headache, fever, and drug overdose), then how can we assign a dummy variables like 1,2,3 to each of them? Why not 1,2, and 23? See the problem?
2. Even if we have two possible response values(0 and 1), then still it’s not that simple. The linear regression can output out of range $[0,1]$, then how do we interpret it? It would be cool to have a function that outputs only between $[0,1]$ and fit the data to it.

Logistic Regression

---

Logistic Regression models the probability of the response falling into one of the two categories. That’s why it always outputs $[0,1]$.

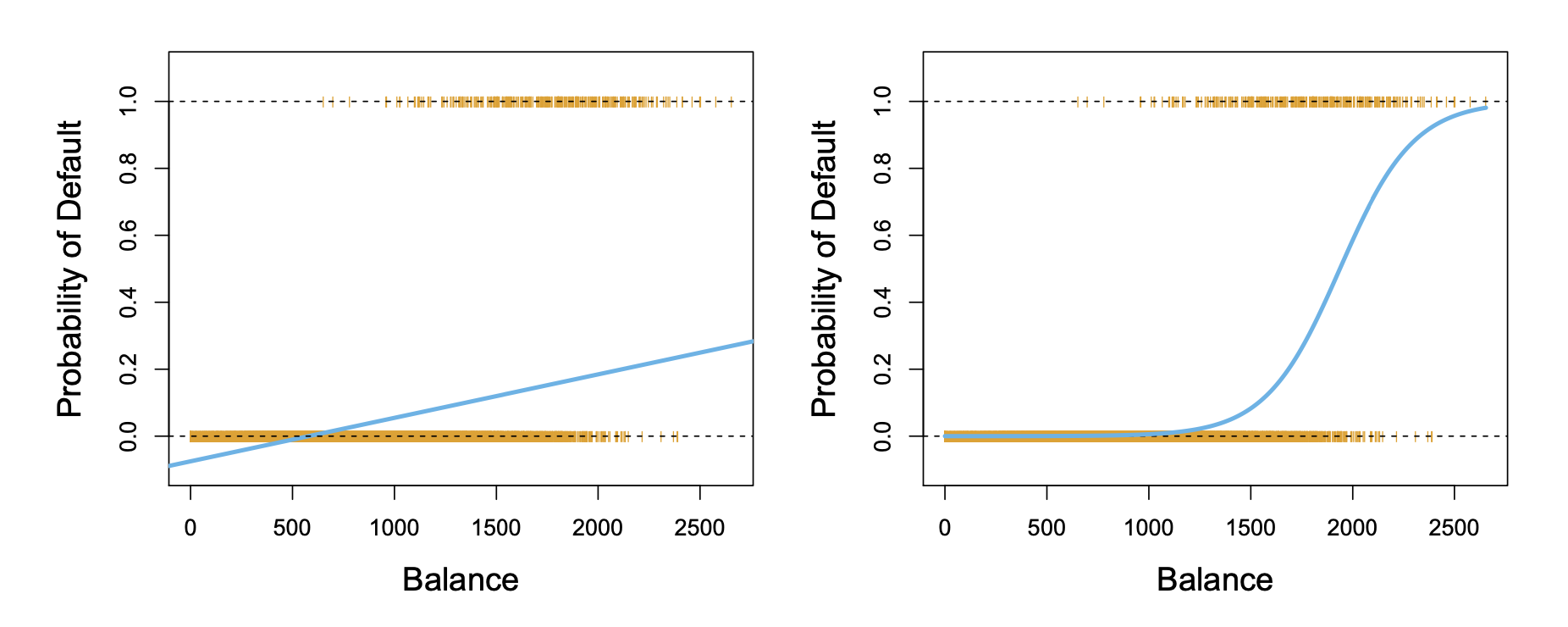
We use the logistic function (s-shaped):

$$p(X)=\frac{e^{{\beta }_0+{\beta }_1\cdot X}}{1+e^{{\beta }_0+{\beta }_1\cdot X}}$$

For example, given $X$ (bank balance account), we might predict $p$, probability of defaulting. The coefficients are estimated by maximum likelihood. We search for betas such that the result we observe (training data) is the most probable. For the binary case, mathematically we try to maximize the function:

$$l({\beta }_0,{\beta }_1)=\Pi p(x_i)\cdot \Pi (1-p(x_{i^{\prime }}))$$

As we can see we assume that the events are independent.

Multiple Regression : It’s not that complicated to guess the form of multiple linear regression: we just add some terms to the power of the exponent.

Generative Models for classification

---

We can use a cool trick, Bayes’ theorem, to flip cards around. For instance, let’s assume we have $k$ classes. Then we can define a function $f_k(x)\equiv Pr(x=X|Y=k)$. What this says is that given Y falls into kth bin, we can find the probability that $x\approx X$. Then Bayes’ theorem states that

$$Pr(Y=k|X=x)=\frac{{\pi }_k{f}_k(x)}{{\sum }_{l=1}^K{\pi }_k{f}_k(x)}$$

(1) State the difference between Bayes classifier and Bayes’ theorem. Two absolutely different things. The problem now arises with finding the $f_k(x)$…

LDA for p = 1

---

One way to do it is use LDA (linear discriminant analysis). (2) What are its main assumptions? Paste the picture of derivation …

For the cases where $p>1$, we assume multivariate Gaussian. Long story short, everything is sort of similar to p=1, but just in multiple dimensions with matrices and vectors. Nothing that much complicated (LUL).

QDA

---

The main difference between LDA and QDA is that the latter does not assume identical covariance matrices for all predictors. Basically, each multidimensional Gaussian has its own unique variance/deviation. From that it attains an additional x-term $\to$ quadratic in the name.

Why not use QDA always since it’s more general method? The answer is again Bias-Variance Trade-off ! (3) At this point you tell me which model is more flexible, has higher variance and bias.

Naive Bayes

---

The problem we face is modeling p-dimensional density function for each $k$ class, which is a hard task. LDA and QDA assumed that these belong to particular family of function (normal). In Naive Bayes, however, we make a different assumption: within $k$ classes, all $p$ predictors are independent!:

$$f_k(x)=f_{k1}(x_1)\times f_{k2}(x_2)\times f_{k3}(x_3)...$$

where each function is single variable: function of the jth predictor on kth class. Now, instead of one p-dimensional problem, we deal with p one-dimensional problems! And here we can once again assume that each function is normal, non-parametric, or qualitative.

Answers

---

1. asdasd
2. First, we assume that $f_k(x)$ is Gaussian and second that standard deviations for each class ${\sigma }_k$ are identical.
3. Obviously (never thought I would start an explanation like that), QDA is more flexible than LDA, and thus has less bias. But this means it depends more on the test data set, which leads to higher variance. Generally, use QDA when an assumption of common covariance matrix might be off or when the data set is large.