Bias-Variance Trade-off

First, we should answer the question: how do we know if a model performs well? One way to do it is to compute the Mean Squared Error (MSE):

$$\text{MSE}=\frac{1}{n}\sum _1^n(y_i-\hat{f}(x_i){)}^2$$

Important point is that we compute MSE by using test data that was not used to train a model. (1) Why so ? If we don’t have a test data, then one might imagine choosing a model that minimizes the MSE for a training data. (2) What problem do we face then? (3) Recall the general pattern/graph between MSE and flexibility. Hint: just explain the U-shaped graph.

Bias-Variance Trade-off

---

The expected test MSE can be decomposed into three fundamental quantities (no proof) like variance, bias, and variance of the error.

$$\text{MSE}=\text{Var}(\hat{f})+[\text{Bias}(\hat{f}){]}^2+\text{Var}(ϵ)$$

The last term is inherently random, and we can’t really get rid of it. Whereas first two terms can be minimized, but it’s still tricky. (4) Intuitively, what is variance and bias of $\hat{f}?$ (5) What’s the connection between them and flexibility? Alternatively, just explain what’s happening in the graph: black is the real $f$, orange is linear regression.

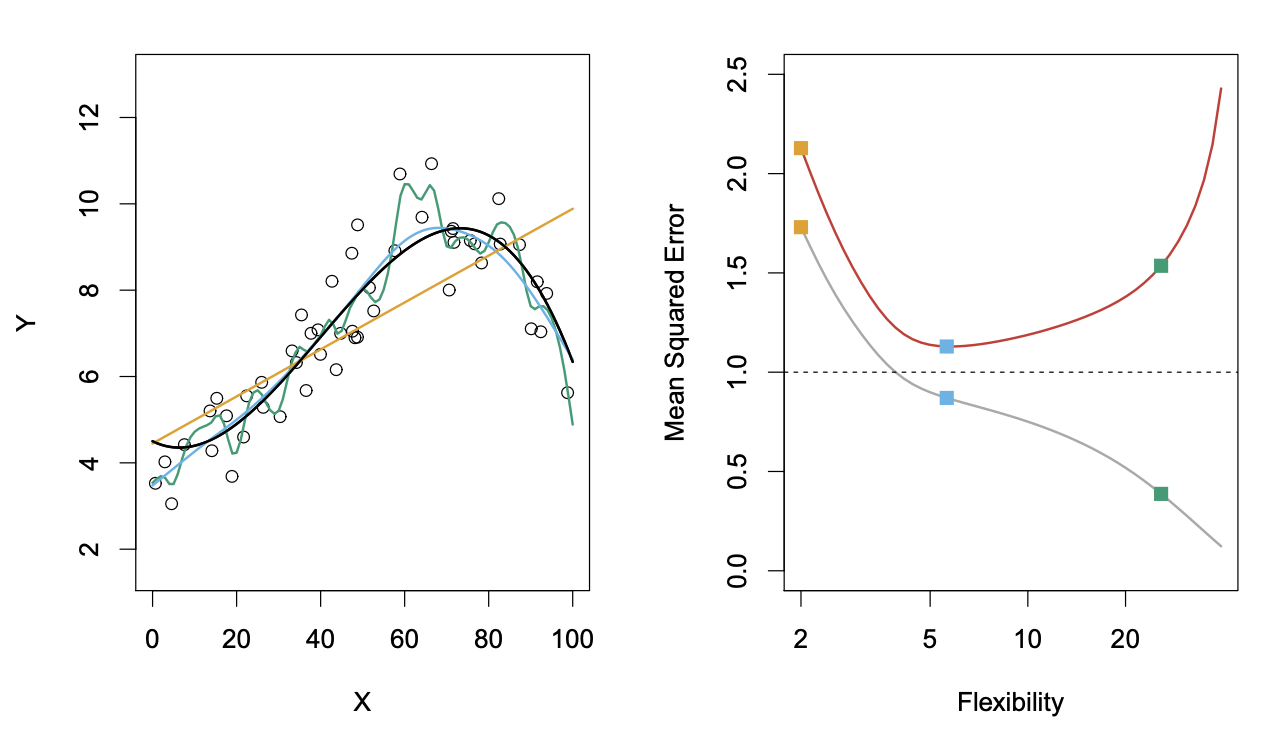
Answers

---

4. Variance refers to a variation of the predicted value by $\hat{f}$ if we used a different data set to train it. Bias refers to an error introduced by approximation/simplification that a model uses.
5. More flexible method $\to$ low bias, but high variance. Not a flexible method $\to$ low variance, but high bias.