Electric Potential

We can define a scalar quantity $\varphi$ to be the line integral of $\text{E}$ between two point:

$${\varphi }_{12}=-{\int }_{P1}^{P2}\text{E}\cdot d\text{l}$$

First, explain why is the line integral path-independent, considering the field of a single point below (1).

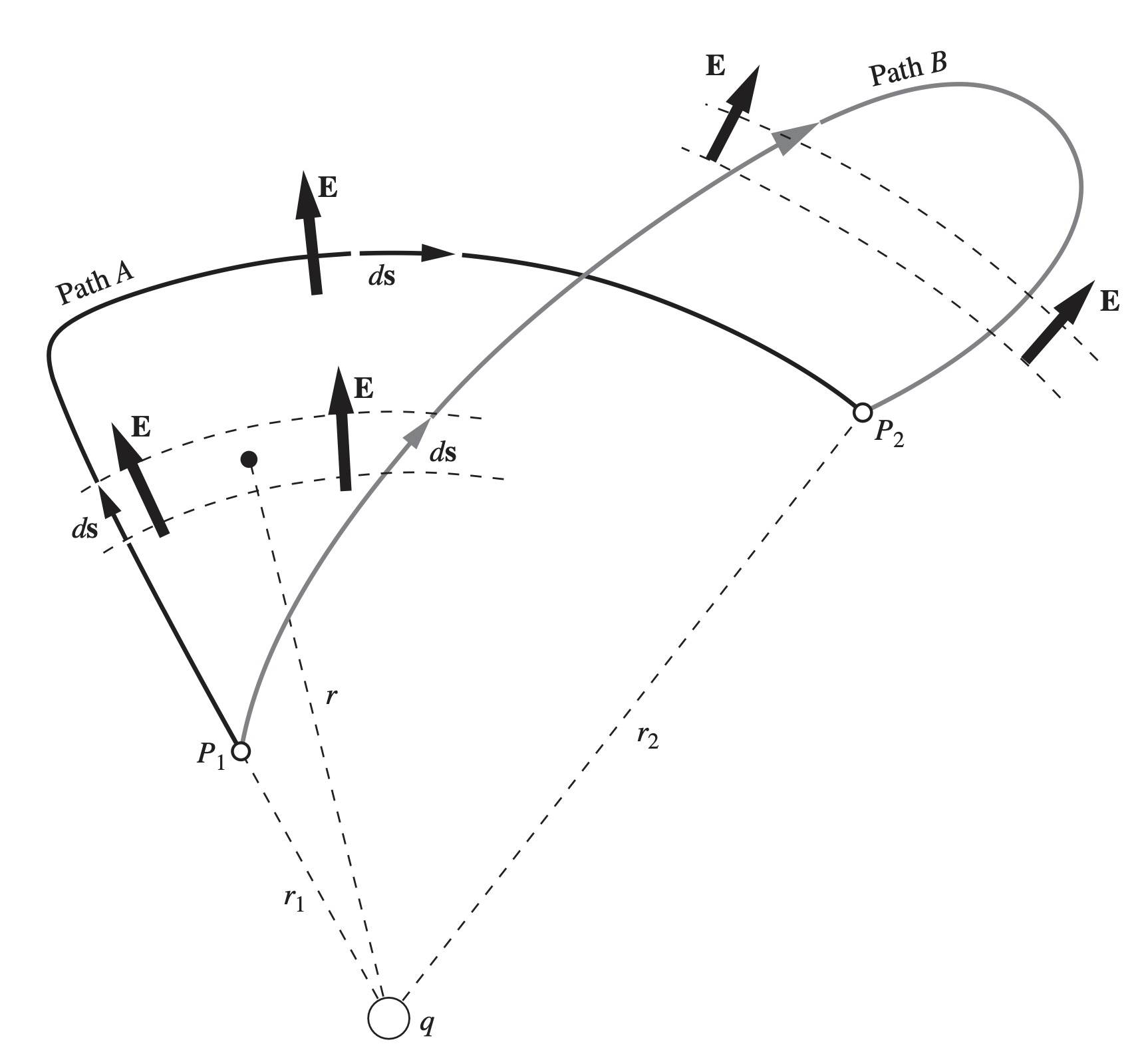
Second, explain how it extends to a general field $\text{E}$ (2). Holding P1 constant we obtain a scalar function $\varphi (x,y,z)$. We can mathematically prove that since $\text{E}$ is a conservative field (Electrostatics. Charges, Energy and Fields), it must be a gradient of some function $f$, and $\varphi$ we defined is that function: $-\nabla \varphi =\text{E}$. Generally, for a localized system of charges potential can be calculated by:

$$\varphi =-{\int }_V\frac{\rho \cdot dv}{4\pi {ϵ}_{0}r}$$

One interesting exercise is to calculate the potential on the rim of a charged disk (Ex 4 in Chapter 2). Key point was to splice the ring into wedges with varying length $l=2a\cos (\theta )$.

Very cool property that follows from math, but can be also explained physically is that electric field is perpendicular to equipotential surface. First, think about the climbing up the hill. Second, the statement must be true, because if $\text{E}$ had a parallel component then it would require some energy to move charge along the equipotential surface.

Problems

---

Some nice exercises to redo are 2.63, 2.57, 2.46, 2.25, 2.13 (Problems solved about Electric potential (Purcell Ch.2)).

Answers

---

1. It is clear that the path A value is $\varphi =\frac{q}{4\pi {ϵ}_0}\cdot (\frac{1}{r_1}-\frac{1}{r_2})$ because we integrate $Edr$. For path B, we have $\int \text{E}\cdot d\text{s}=\int Eds\cos (\theta )=\int Edr$.
2. Let’s consider the case of the line integral around the two charges. By superposition principle Electrostatics. Charges, Energy and Fields, the field $\text{E}={\text{E}}_1+{\text{E}}_2$. So, the integral is decomposed into to $\int \text{E}\cdot d\text{s}=\int ({\text{E}}_1+{\text{E}}_2)\cdot d\text{s}=$