Electrostatics. Charges, Energy and Fields

If we have two charges $q_1,q_2$ , then the interaction between them is described by Coulomb’s law.

$${\text{F}}_2=\frac{q_1{q}_2}{4\pi {ϵ}_0{r}^2}\cdot \widehat{r_{12}}$$

where the unit vector is pointed from $q_1$ to $q_2$. One of the foundational observations is that Coulomb’s law is additive, which means that no matter how many charges we have in our system we can use Coulomb’s law to calculate the interaction between them. If we have 3 charges ($q_1,q_2,q_3$), what is the force on $q_3$ (1)? The additivity of Coulomb’s law leads to Superposition principle.

Energy

---

Now, imagine we have a charge $q_1$, and we bring $q_2$ to it from infinitely far distance. How much energy does it take us to bring it to distance $r$? Well, work done is

$$W={\int }_C\text{F}\cdot d\text{s}$$

, where C is the curve (path or line) we take. Let’s consider the easiest path $\to$ straight line.

$$W={\int }_{\infty }^{r}Fdr={\int }_{\infty }^r\frac{q_1{q}_2}{4\pi {ϵ}_0{r}^2}dr=-\frac{q_1{q}_2}{4\pi {ϵ}_{0}r}$$

I forgot about the minus sign: how do we get rid of it (2)? We claim that no matter what path we take the integral calculated above is the same. So, wiggle the electron as you wish, but the $W$ does not change! This can be proven in many ways, but one is to show that Vector Field of the Force is conservative. So, take the curl! ($\nabla \times \vec{F}$) (3)

Electric field

---

Now, imagine we collect bunch of charges (N). We then ask the question what force would our collection of charges exert on other charge $q$ located at $x,y,z$? This is where we introduce electric fields, basically it’s the force field divided by unit charge. So, the force on $q$

$$F=\sum _i^N\frac{q_{i}q}{4\pi {ϵ}_0{r}_i^2}$$

and the field is

$$\text{E}(x,y,z)=\sum _i^N\frac{q_i}{4\pi {ϵ}_0{r}_i^2}$$

This is a vector field, which means that it is a function that assigns to every point in space (x,y,z) a vector. Take a minute to digest this information. Below is the field of a positive charge. At each point it shows the direction and relative magnitude of force per unit charge.

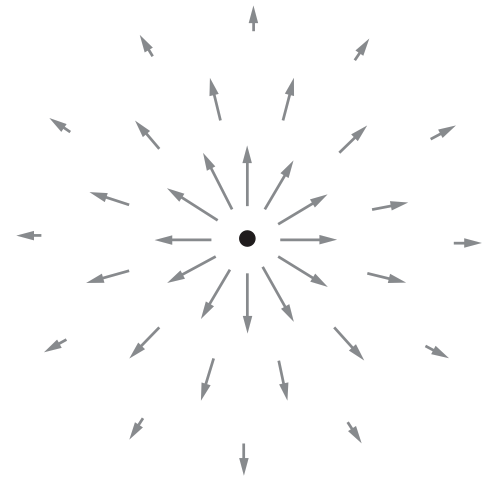Now, imagine we have a body that is described by the charge density function $\rho (x,y,z)$ (e.g banana). We can calculate the field of this object by moving from discrete sum to continuous (integral):

$$\text{E}=\frac{1}{4\pi {ϵ}_0}{\int }_V\frac{\rho (x,y,z)dxdydz}{r^2}\hat{r}$$

Problem

---

We end this note by solving a problem, which made me suffer a lot when I first encountered it. What is the field of a hemisphere with uniform density $\rho$ at its center?

The book has the solution, but I want to discuss one moment of it here since I didn’t get it at all when I read it. The trickiest part here is to move into spherical coordinates. In Cartesian coordinates infinitesimal box has a volume $dxdydz$, but in Polar coordinates it is $r^2\sin (\varphi )drd\theta d\varphi$ (Soon, in a separate note I will show why it’s true mathematically). So, the integral becomes

$$\text{E}=\frac{1}{4\pi {ϵ}_0}{\int }_V\frac{\rho \cdot r^2\sin (\varphi )drd\theta d\varphi }{r^2}\hat{r}$$

The last nuance is related to the direction! We have multiply by $\cos (\theta )$. Why? By symmetry, it has to point above (not down, because it repels). So, when we sum we only care about the vertical component because horizontal ones cancel anyway. This is where additional $\cos (\theta )$ comes from. It took me quite a bit to fully understand this, so when you read it first time, you might as well leave it to come back later with more experience. To practice similar set of skills, look at problems 1.12, 1.14 Problems solved about Electrostatics (Purcell Ch. 1)

Answer to Questions

---

$${\text{F}}_3=\frac{q_1{q}_3}{4\pi {ϵ}_0{r}_{13}^2}\cdot {\hat{r}}_{13}+\frac{q_2{q}_3}{4\pi {ϵ}_0{r}_{23}^2}\cdot {\hat{r}}_{23}$$

2. The actual integral had a applied force multiplied by a distance. We took Coulomb’s force which is the opposite.
3. Curl would be zero, which from multivariable calculus Conservative Vector Fields is equivalent to the fact that the line integral between to two points is the same independent of a path taken.