Understanding Deep Learning Textbook

In this note, I’ll share notes that I found insightful and interesting while reading Understanding Deep Learning, which I found through MIT’s public course on the subject.

Currently, I am at Chapter 9, and I’ll update the notes as I review my notes.

Ch. 1 - 2

The first two chapters just explain the big picture and show how to train a linear regression model (in 2 dimensions). Nothing that much interesting.

Time spent: 1 hour

Ch 3: Shallow neural networks

Time spent: 2.5 hours

The basics

The prelude to the fun begins here. Shallow neural networks have just 1 hidden layer with many hidden units. In the book, they consider an example with 3 hidden units (with 1d input and output), and the general formula for such a neural net would be

$$y={\varphi }_0+{\varphi }_1\cdot a[{\theta }_{10}+{\theta }_{11}x]+{\varphi }_2\cdot a[{\theta }_{20}+{\theta }_{21}x]+{\varphi }_3\cdot a[{\theta }_{30}+{\theta }_{31}x]$$

where $a$ is the activation function, and most of the time it’s just ReLU. The interpretation/intuition of building them up is the key. If you define the hidden units as outputs of the activation function, as

$$\begin{array}{r}{h}_1=a[{\theta }_{10}+{\theta }_{11}x]\\ h_2=a[{\theta }_{20}+{\theta }_{21}x]\\ h_3=a[{\theta }_{30}+{\theta }_{31}x]\end{array}$$

then each of these $h_i$‘s are clipped linear function. The final output is just a linear combination of these hidden units (aka each is scaled by ${\varphi }_i$ and a bias term ${\varphi }_0$ is added). The whole pipeline is depicted below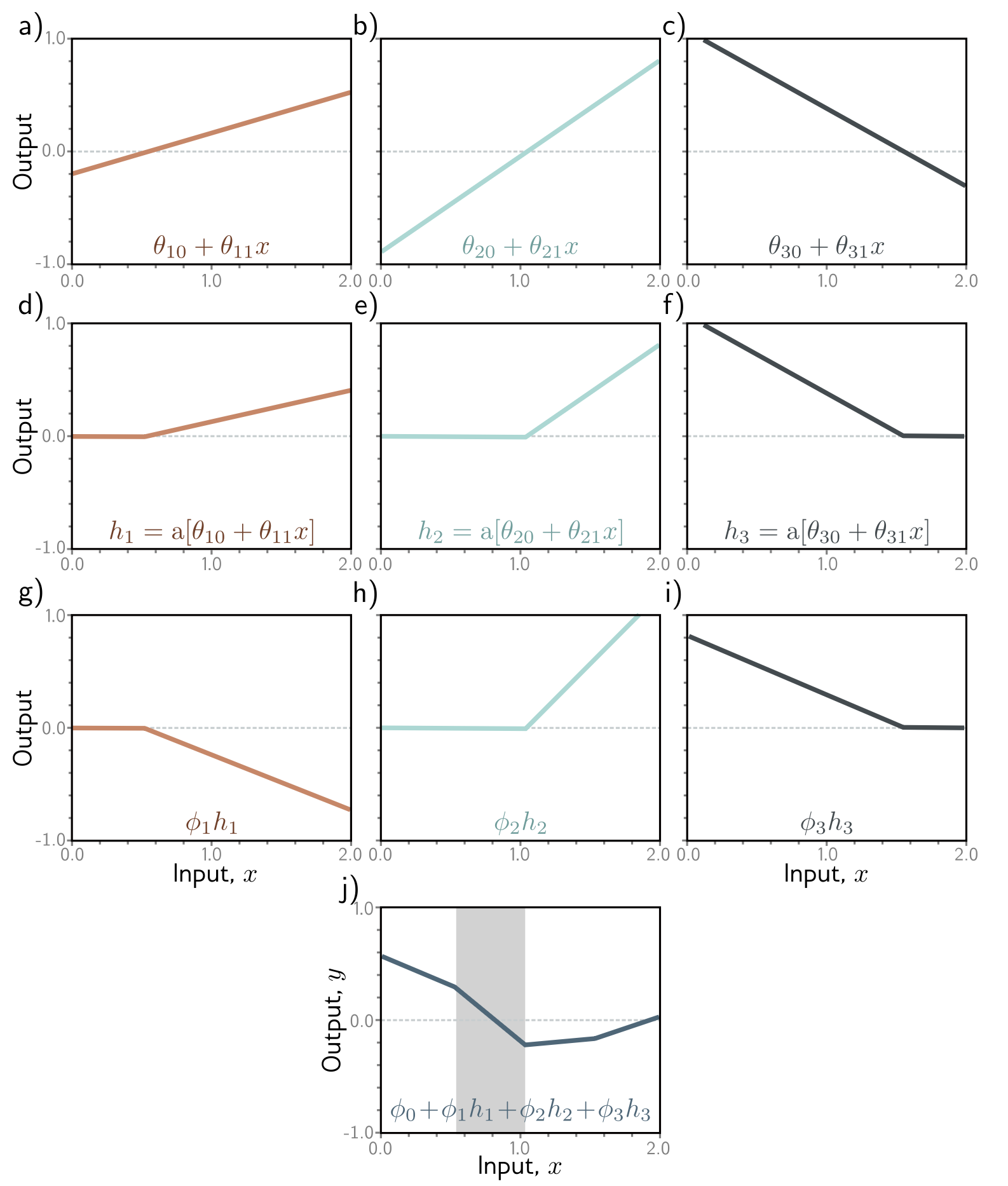

As you can see the more hidden units you add the more joints you have in the final function, which is a piecewise linear function. This can be formalized in Universal Approximation Theorem, which states that any function (in any dimension!) can be approximated by a Shallow neural net. In practice, to approximate a complicated function you would need a LOT of hidden units, and that’s where Deep neural nets win over.

General case

In the multivariate input and output, the formula can be written as

$$\begin{array}{r}{h}_d=a\left[{\theta }_{d0}+\sum _{i=1}^{D_i}{\theta }_{di}{x}_i\right]\\ y_j={\varphi }_{j0}+\sum _{d=1}^D{\varphi }_{jd}{h}_d\end{array}$$

where $D_i$ is the input dimension, $D$ is the number of hidden units. The clean way to write is to recognize the matrix multiplication in the sum:

$$\begin{array}{r}\text{h}=a[{\mathbf{b}}_0+\mathbf{Wx}]\\ \text{y}={\mathbf{b}}_1+\mathbf{\Phi h}\end{array}$$

where $\mathbf{W}$ is a matrix of $D\times D_i$, and $\mathbf{\Phi }$ is a matrix of $D_0\times D$, and non-linear activation acts point-wise. One of the problems with Shallow neural nets and multivariate outputs is that $y_1,y_2$ would have ‘joints’ at the same points! You see how this is a problem, if number of hidden units is not huge?

Number of regions vs hidden units

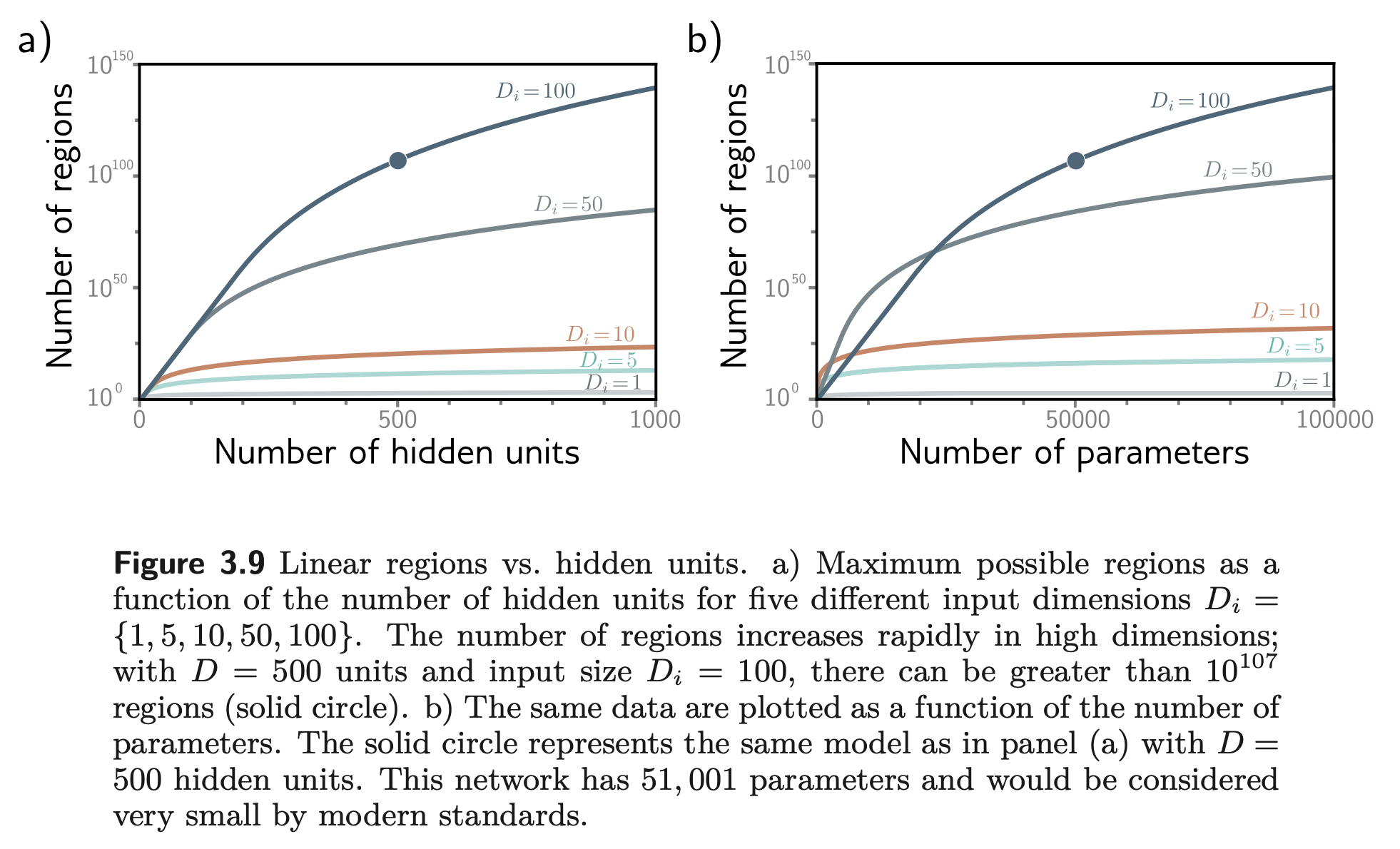
Note that the higher the input dimension, the more linear regions you get. Intuitively, that kind of makes sense because in higher dimensions linear ‘regions’ become linear hyperplanes, and when you add them up, there are just more ways they can intersect. Quick estimation that I really like: let’s say we have $D_i=D$, and each hyperplane gets activated along one of the axes. In 1D, you get activation at x=0, and $2^1$ linear regions. In 2D, you get activation at x=0 (line!), y=0 (line!) and you generate $2^2=4$ linear regions. In 3D, you basically intersect 3 planes, and get $2^3=8$ octants. I guess, you see the pattern. You can create $2^{D_i}$ linear regions !!!

Ch 4: Deep neural networks

*Time spent: 2.0 hours